遍历二叉树：L、D、R分别表示遍历左子树、访问根结点和遍历右子树，则先(根)序遍历二叉树的顺序是DLR，中(根)序遍历二叉树的顺序是LDR，后(根)序遍历二叉树的顺序是LRD。还有按层遍历二叉树。这些方法的时间复杂度都是O(n)，n为结点个数。

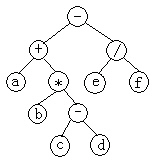
用二叉树表示上述表达式：a+b*(c-d)-e/f

• 先序遍历的序列是：-+a*b-cd/ef
• 中序遍历的序列是：a+b*c-d-e/f
• 后序遍历的序列是：abcd-*+ef/-

二叉树的存储

1.顺序存储

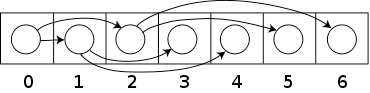
二叉树可以用数组或线性表来存储，而且如果这是满二叉树，这种方法不会浪费空间。用这种紧凑排列，如果一个结点的索引为i，它的子结点能在索引2i+1和2i+2找到，并且它的父节点（如果有）能在索引floor((i-1)/2)找到（假设根节点的索引为0）。

2.二叉链表存储

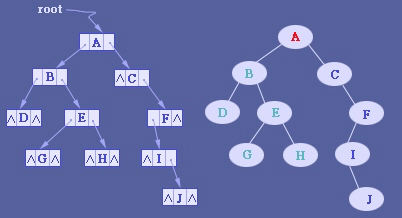
二叉树通常用树结点结构来存储。有时也包含指向唯一的父节点的指针。如果一个结点的子结点个数小于2，一些子结点指针可能为空值，或者为特殊的哨兵结点。 使用链表能避免顺序储存浪费空间的问题，算法和结构相对简单，但使用二叉链表，由于缺乏父链的指引，在找回父节点时需要重新扫描树得知父节点的节点地址。

3.三叉链表存储

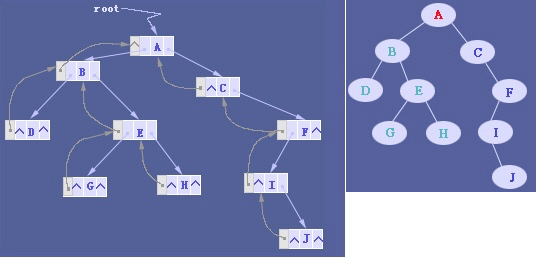
改进于二叉链表，增加父节点的指引，能更好地实现节点间的访问，不过算法相对复杂。 当二叉树用三叉链表表示时，有N个结点，就会有N+2个空指针。

前中后续遍历（递归）

/* 
 *前序遍历二叉树 
 * */  
public void preOrder(Node node){  
        if(node != null){  
            System.out.print(node.data);  
            preOrder(node.leftChild);  
            preOrder(node.rightChild);  
        }  
}  
/* 
 *中序遍历二叉树 
 * */  
public void inOrder(Node node){  
        if(node != null){  
            inOrder(node.leftChild);  
            System.out.print(node.data);  
            inOrder(node.rightChild);  
        }  
}  
/* 
 *后序遍历二叉树 
 * */  
public void postOrder(Node node){  
        if(node != null){  
            postOrder(node.leftChild);  
            postOrder(node.rightChild);  
            System.out.print(node.data);              
}

前中后续遍历（非递归）

/** 
  *  
  * 【前序】
  * 利用栈实现循环先序遍历二叉树 
  * 这种实现类似于图的深度优先遍历（DFS） 
  * 维护一个栈，将根节点入栈，然后只要栈不为空，出栈并访问，接着依次将访问节点的右节点、左节点入栈。 
  * 这种方式应该是对先序遍历的一种特殊实现（看上去简单明了），但是不具备很好的扩展性，在中序和后序方式中不适用 
  */  
public static void preOrderStack(Node root){  
        if(root==null)return;  
        Stack<Node> s=new Stack<Node>();  
        s.push(root);  
        while(!s.isEmpty()){  
            Node temp=s.pop();  
            System.out.println(temp.value);  
            if(temp.right!=null) s.push(temp.right);  
            if(temp.left!=null) s.push(temp.left);  
        }  
}

/** 
  *  
  * 【中序】
  * 利用栈模拟递归过程实现循环中序遍历二叉树 
  * 访问的时间是在左子树都处理完直到null的时候出栈并访问。 
  */  
public static void inOrderStack(Node root){  
        if(root==null)return;  
        Stack<Node> s=new Stack<Node>();  
        while(root!=null||!s.isEmpty()){  
            while(root!=null){  
                s.push(root);//先访问再入栈  
                root=root.left;  
            }  
            root=s.pop();  
            System.out.println(root.value);  
            root=root.right;//如果是null，出栈并处理右子树  
        }  
}

/** 
  *  
  * 【后续】
  * 后序遍历不同于先序和中序，它是要先处理完左右子树，然后再处理根(回溯)，所以需要一个记录哪些节点已经被访问的结构(可以在树结构里面加一个标记)，这里可以用map实现 
  */  
public static void postOrderStack(Node root){  
        if(root==null)return;  
        Stack<Node> s=new Stack<Node>();  
        Map<Node,Boolean> map=new HashMap<Node,Boolean>();   
        s.push(root);  
        while(!s.isEmpty()){  
            Node temp=s.peek();  
            if(temp.left!=null&&!map.containsKey(temp.left)){  
                temp=temp.left;  
                while(temp!=null){  
                    if(map.containsKey(temp))break;  
                    else s.push(temp);  
                    temp=temp.left;  
                }  
                continue;  
            }  
            if(temp.right!=null&&!map.containsKey(temp.right)){  
                s.push(temp.right);  
                continue;  
            }  
            Node t=s.pop();  
            map.put(t,true);  
            System.out.println(t.value);  
        }  
}

广度优先遍历（层次遍历）

/** 
  * @param root 树根节点 
  * 层序遍历二叉树，用队列实现，先将根节点入队列，只要队列不为空，然后出队列，并访问，接着讲访问节点的左右子树依次入队列 
  */  
public static void levelTravel(Node root){  
        if(root==null)return;  
        Queue<Node> q=new LinkedList<Node>();  
        q.add(root);  
        while(!q.isEmpty()){  
            Node temp =  q.poll();  
            System.out.println(temp.value);  
            if(temp.left!=null)q.add(temp.left);  
            if(temp.right!=null)q.add(temp.right);  
        }  
}