使用了广度优先搜索解决非负权有向图的单源最短路径问题，算法最终得到一个最短路径树（一个节点到其他所有节点的最短路径）。该算法常用于路由算法或者作为其他图算法的一个子模块。主要特点是以起始点为中心向外层层扩展，直到扩展到终点为止。

算法思想：

设G=(V,E)是一个带权有向图，把图中顶点集合V分成两组，第一组为已求出最短路径的顶点集合（用S表示，初始时S中只有一个源点，以后每求得一条最短路径 , 就将加入到集合S中，直到全部顶点都加入到S中，算法就结束了）

第二组为其余未确定最短路径的顶点集合（用U表示），按最短路径长度的递增次序依次把第二组的顶点加入S中。在加入的过程中，总保持从源点v到S中各顶点的最短路径长度不大于从源点v到U中任何顶点的最短路径长度。此外，每个顶点对应一个距离，S中的顶点的距离就是从v到此顶点的最短路径长度，U中的顶点的距离，是从v到此顶点只包括S中的顶点为中间顶点的当前最短路径长度。

算法步骤：

1. 初始时，S只包含源点，即S＝{v}，v的距离为0。U包含除v外的其他顶点，即:U={其余顶点}，若v与U中顶点u有边，则（u,v）正常有权值，若u不是v的出边邻接点，则（u,v）权值为∞。

2. 从U中选取一个距离v最小的顶点k，把k，加入S中（该选定的距离就是v到k的最短路径长度）。

3. 以k为新考虑的中间点，修改U中各顶点的距离；若从源点v到顶点u的距离（经过顶点k）比原来距离（不经过顶点k）短，则修改顶点u的距离值，修改后的距离值的顶点k的距离加上边上的权。

4. 重复步骤2和3直到所有顶点都包含在S中。

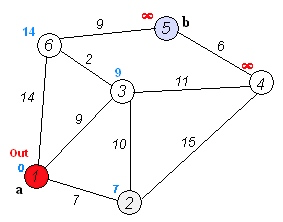Dijkstra算法（Java实现）

public class Dijkstra {
    private static int M = 10000; //此路不通

    public static void main(String[] args) {
        //邻接矩阵
        int[][] weight = {
                {0, 10, M, 30, 100},
                {M, 0, 50, M, M},
                {M, M, 0, M, 10},
                {M, M, 20, 0, 60},
                {M, M, M, M, 0}
        };

        int start = 0;
        int[] shortPath = dijkstra(weight, start);

        for (int i = 0; i < shortPath.length; i++)
            System.out.println("从" + start + "出发到" + i + "的最短距离为：" + shortPath[i]);
    }

    public static int[] dijkstra(int[][] weight, int start) {
        //接受一个有向图的权重矩阵，和一个起点编号start（从0编号，顶点存在数组中）
        //返回一个int[] 数组，表示从start到它的最短路径长度
        int n = weight.length;      //顶点个数
        int[] shortPath = new int[n];  //保存start到其他各点的最短路径
        String[] path = new String[n];  //保存start到其他各点最短路径的字符串表示
        for (int i = 0; i < n; i++)
            path[i] = new String(start + "-->" + i);
        int[] visited = new int[n];   //标记当前该顶点的最短路径是否已经求出,1表示已求出

        //初始化，第一个顶点已经求出
        shortPath[start] = 0;
        visited[start] = 1;

        for (int count = 1; count < n; count++) {   //要加入n-1个顶点
            int k = -1;        //选出一个距离初始顶点start最近的未标记顶点
            int dmin = Integer.MAX_VALUE;
            for (int i = 0; i < n; i++) {
                if (visited[i] == 0 && weight[start][i] < dmin) {
                    dmin = weight[start][i];
                    k = i;
                }
            }

            //将新选出的顶点标记为已求出最短路径，且到start的最短路径就是dmin
            shortPath[k] = dmin;
            visited[k] = 1;

            //以k为中间点，修正从start到未访问各点的距离
            for (int i = 0; i < n; i++) {
                if (visited[i] == 0 && weight[start][k] + weight[k][i] < weight[start][i]) {
                    weight[start][i] = weight[start][k] + weight[k][i];
                    path[i] = path[k] + "-->" + i;
                }
            }
        }
        for (int i = 0; i < n; i++) {
            System.out.println("从" + start + "出发到" + i + "的最短路径为：" + path[i]);
        }
        System.out.println("=====================================");
        return shortPath;
    }
}

运行结果：

从0出发到0的最短路径为：0-->0
从0出发到1的最短路径为：0-->1
从0出发到2的最短路径为：0-->3-->2
从0出发到3的最短路径为：0-->3
从0出发到4的最短路径为：0-->3-->2-->4
=====================================
从0出发到0的最短距离为：0
从0出发到1的最短距离为：10
从0出发到2的最短距离为：50
从0出发到3的最短距离为：30
从0出发到4的最短距离为：60